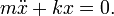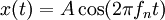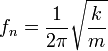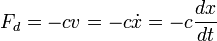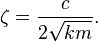Minggu, 25 Juli 2010
Selasa, 20 Juli 2010
Hukum Baru dalam Fisika Modern
Hee..pernah denger sebuah teori tentan efek fotolistrik? Ternyata salah satu bagian dari fisika modern ini jika diteliti lagi dapat menghasilkan sebuah hukum baru yang akan membuat Anda menggeleng-geleng antara percaya dan tidak. Tentu setelah efek ini disatukan dengan sebuah efek lain yang terkait. Apakah itu? Mari simak penjelasannya berikut.
Efek fotolistrik adalah salah satu bahasan dalam fisika modern terkait dualisme partikel-gelombang. Aspek penting dalam efek fotolistrik adalah ketika dilakukan observasi pertamanya bahwa:
1. elektron langsung dipancarkan.
2. meningkatnya intensitas cahaya meningkatkan jumlah fotolistrik tapi tidak sampai pada energi kinetik maksimumnya.
3. sinar merah tidak menyebabkan penyemburan elektron berapapun intensitasnya.
4. sinar ungu yang lemah akan memancarkan sedikit elektron, tapi energi kinetik maksimumnya lebih tinggi daripada cahaya yang memiliki panjang gelombang lebih panjang.
Setidaknya itu poin pentingnya. Nah, jika kemudian dilakukan sebuah observasi lain dengan menambahkan gelombang bunyi dari speaker pc, maka akan menimbulkan sebuah efek perubahan di gelombang otak yang menyebabkan Anda akan merasakan ketenangan sekaligus kecemasan. Mengapa ini bisa terjadi? Ternyata hal ini disebabkan efek fotolistrik menimbulkan perubahan gelombang pada otak Anda dan Anda merasakan kecemasan akibat harus dipahaminya konsep secara menyeluruh. Sedangkan gelombang bunyi yang berasal dari speaker pc merupakan lantunan musik bernuansa cinta, persahabatan dan rasa. Hal ini antara lain menyebabkan gelombang dalam otak Anda akan mengalami ketenangan, namun terkadang membuat Anda merasa sedih atau kecewa.
Dari hasil observasi inilah muncul sebuah konsep baru bernama Hukum meusiseu I yang merupakan sebuah konsep yang perlu dipahami oleh setiap mahasiswa Teknik Informatika yang sedang belajar Fisika Komputasi.
Hukum meusiseu I ini berbunyi, “Ketika sindrom fisika modern memasuki kehidupan Anda dan efek fotolistrik mempengaruhi kehidupan Anda, maka jauhkanlah gelombang bunyi bernuansa cinta atau dikenal dengan lagu mellow karena hal ini akan menimbulkan efek meusiseu*.”
*meusiseu diambil dari istilah bahasa aceh, dalam bahasa Indonesia berarti berantakan.
Kamis, 15 Juli 2010
GERAK HARMONIK SEDERHANA
Gerak Harmonik Sederhana
 Pengantar
Pengantar
Dalam kehidupan sehari-hari terdapat banyak benda yang bergetar. Senar gitar yang sering anda main atau dimainkan oleh gitaris group band musik terkenal yang kadang membuat anda menjerit histeris bahkan sampai menangis tersedu-sedu, getaran garpu tala, getaran mobil ketika mesinnya dinyalakan atau ketika mobil mencium mobil lainnya hingga penumpangnya babak belur. Ingat juga ketika anda tertawa terpingkal-pingkal tubuh anda juga bergetar, demikian juga rumah anda yang bergetar dasyat hingga ambruk ketika terjadi gempa bumi. Sangat banyak contoh getaran dalam kehidupan kita, sehingga jika disebutkan satu persatu maka tentu sangat melelahkan. Silahkan dipikirkan sendiri contoh lainnya.
Getaran dan gelombang merupakan dua hal yang saling berkaitan. Gelombang, baik itu gelombang air laut, gelombang gempa bumi, gelombang suara yang merambat di udara; semuanya bersumber pada getaran. Dengan kata lain, getaran adalah penyebab adanya gelombang. Mengenai gelombang, selengkapnya akan kita pelajari pada pokok bahasan tersendiri. Sekarang terlebih dahulu kita pelajari pokok bahasan getaran. Semoga setelah mempelajari getaran, dirimu tidak ikut bergetar, apalagi ketika gurumu menyajikan soal-soal hitungan yang membuat dirimu mabuk kepayang.
Setiap gerak yang terjadi secara berulang dalam selang waktu yang sama disebut gerak periodik. Karena gerak ini terjadi secara teratur maka disebut juga sebagai gerak harmonik/harmonis. Apabila suatu partikel melakukan gerak periodik pada lintasan yang sama maka geraknya disebut gerak osilasi/getaran. Bentuk yang sederhana dari gerak periodik adalah benda yang berosilasi pada ujung pegas. Karenanya kita menyebutnya gerak harmonis sederhana. Banyak jenis gerak lain (osilasi dawai, roda keseimbangan arloji, atom dalam molekul, dan sebagainya) yang mirip dengan jenis gerakan ini, sehingga pada kesempatan ini kita akan membahasnya secara mendetail.
Dalam kehidupan sehari-hari, gerak bolak balik benda yang bergetar terjadi tidak tepat sama karena pengaruh gaya gesekan. Ketika kita memainkan gitar, senar gitar tersebut akan berhenti bergetar apabila kita menghentikan petikan. Demikian juga bandul yang berhenti berayun jika tidak digerakan secara berulang. Hal ini disebabkan karena adanya gaya gesekan. Gaya gesekan menyebabkan benda-benda tersebut berhenti berosilasi. Jenis getaran seperti ini disebut getaran harmonik teredam. Walaupun kita tidak dapat menghindari gesekan, kita dapat meniadakan efek redaman dengan menambahkan energi ke dalam sistem yang berosilasi untuk mengisi kembali energi yang hilang akibat gesekan, salah satu contohnya adalah pegas dalam arloji yang sering kita pakai. Pada kesempatan ini kita hanya membahas gerak harmonik sederhana secara mendetail, karena dalam kehidupan sehari-hari terdapat banyak jenis gerak yang menyerupai sistem ini.
Gerak harmonis sederhana yang dapat dijumpai dalam kehidupan sehari-hari adalah getaran benda pada pegas dan getaran benda pada ayunan sederhana. Kita akan mempelajarinya satu persatu.
Gerak Harmonis Sederhana pada Ayunan
 Ketika beban digantungkan pada ayunan dan tidak diberikan gaya maka benda akan diam di titik kesetimbangan B. Jika beban ditarik ke titik A dan dilepaskan, maka beban akan bergerak ke B, C, lalu kembali lagi ke A. Gerakan beban akan terjadi berulang secara periodik, dengan kata lain beban pada ayunan di atas melakukan gerak harmonik sederhana.
Ketika beban digantungkan pada ayunan dan tidak diberikan gaya maka benda akan diam di titik kesetimbangan B. Jika beban ditarik ke titik A dan dilepaskan, maka beban akan bergerak ke B, C, lalu kembali lagi ke A. Gerakan beban akan terjadi berulang secara periodik, dengan kata lain beban pada ayunan di atas melakukan gerak harmonik sederhana.
Besaran fisika pada Gerak Harmonik Sederhana pada ayunan sederhana
Benda yang bergerak harmonis sederhana pada ayunan sederhana memiliki periode alias waktu yang dibutuhkan benda untuk melakukan satu getaran secara lengkap. Benda melakukan getaran secara lengkap apabila benda mulai bergerak dari titik di mana benda tersebut dilepaskan dan kembali lagi ke titik tersebut.
Pada contoh di atas, benda mulai bergerak dari titik A lalu ke titik B, titik C dan kembali lagi ke B dan A. Urutannya adalah A-B-C-B-A. Seandainya benda dilepaskan dari titik C maka urutan gerakannya adalah C-B-A-B-C.
Jadi periode ayunan (T) adalah waktu yang diperlukan benda untuk melakukan satu getaran (disebut satu getaran jika benda bergerak dari titik di mana benda tersebut mulai bergerak dan kembali lagi ke titik tersebut ). Satuan periode adalah sekon atau detik.
Selain periode, terdapat juga frekuensi alias banyaknya getaran yang dilakukan oleh benda selama satu detik. Yang dimaksudkan dengan getaran di sini adalah getaran lengkap. Satuan frekuensi adalah 1/sekon atau s-1. 1/sekon atau s-1 disebut juga hertz, menghargai seorang fisikawan. Hertz adalah nama seorang fisikawan tempo doeloe. Silahkan baca biografinya untuk mengenal almahrum eyang Hertz lebih dekat.
Hubungan antara Periode dan Frekuensi
Frekuensi adalah banyaknya getaran yang terjadi selama satu detik/sekon. Dengan demikian selang waktu yang dibutuhkan untuk melakukan satu getaran adalah :![]()
Selang waktu yang dibutuhkan untuk melakukan satu getaran adalah periode. Dengan demikian, secara matematis hubungan antara periode dan frekuensi adalah sebagai berikut :

Amplitudo (f)
Pada ayunan sederhana, selain periode dan frekuensi, terdapat juga amplitudo. Amplitudo adalah perpindahan maksimum dari titik kesetimbangan. Pada contoh ayunan sederhana sesuai dengan gambar di atas, amplitudo getaran adalah jarak AB atau BC.
Gerak Harmonis Sederhana pada Pegas
 Semua pegas memiliki panjang alami sebagaimana tampak pada gambar a. Ketika sebuah benda dihubungkan ke ujung sebuah pegas, maka pegas akan meregang (bertambah panjang) sejauh y. Pegas akan mencapai titik kesetimbangan jika tidak diberikan gaya luar (ditarik atau digoyang), sebagaimana tampak pada gambar B. Jika beban ditarik ke bawah sejauh y1 dan dilepaskan (gambar c), benda akan akan bergerak ke B, ke D lalu kembali ke B dan C. Gerakannya terjadi secara berulang dan periodik. Sekarang mari kita tinjau hubungan antara gaya dan simpangan yang dialami pegas.
Semua pegas memiliki panjang alami sebagaimana tampak pada gambar a. Ketika sebuah benda dihubungkan ke ujung sebuah pegas, maka pegas akan meregang (bertambah panjang) sejauh y. Pegas akan mencapai titik kesetimbangan jika tidak diberikan gaya luar (ditarik atau digoyang), sebagaimana tampak pada gambar B. Jika beban ditarik ke bawah sejauh y1 dan dilepaskan (gambar c), benda akan akan bergerak ke B, ke D lalu kembali ke B dan C. Gerakannya terjadi secara berulang dan periodik. Sekarang mari kita tinjau hubungan antara gaya dan simpangan yang dialami pegas.
Kita tinjau pegas yang dipasang horisontal, di mana pada ujung pegas tersebut dikaitkan sebuah benda bermassa m. Massa benda kita abaikan, demikian juga dengan gaya gesekan, sehingga benda meluncur pada permukaan horisontal tanpa hambatan. Terlebih dahulu kita tetapkan arah positif ke kanan dan arah negatif ke kiri. Setiap pegas memiliki panjang alami, jika pada pegas tersebut tidak diberikan gaya. Pada kedaan ini, benda yang dikaitkan pada ujung pegas berada dalam posisi setimbang (lihat gambar a). Untuk semakin memudahkan pemahaman dirimu,sebaiknya dilakukan juga percobaan.
 Apabila benda ditarik ke kanan sejauh +x (pegas diregangkan), pegas akan memberikan gaya pemulih pada benda tersebut yang arahnya ke kiri sehingga benda kembali ke posisi setimbangnya (gambar b).
Apabila benda ditarik ke kanan sejauh +x (pegas diregangkan), pegas akan memberikan gaya pemulih pada benda tersebut yang arahnya ke kiri sehingga benda kembali ke posisi setimbangnya (gambar b).
 Sebaliknya, jika benda ditarik ke kiri sejauh -x, pegas juga memberikan gaya pemulih untuk mengembalikan benda tersebut ke kanan sehingga benda kembali ke posisi setimbang (gambar c).
Sebaliknya, jika benda ditarik ke kiri sejauh -x, pegas juga memberikan gaya pemulih untuk mengembalikan benda tersebut ke kanan sehingga benda kembali ke posisi setimbang (gambar c). Besar gaya pemulih F ternyata berbanding lurus dengan simpangan x dari pegas yang direntangkan atau ditekan dari posisi setimbang (posisi setimbang ketika x = 0). Secara matematis ditulis :
Besar gaya pemulih F ternyata berbanding lurus dengan simpangan x dari pegas yang direntangkan atau ditekan dari posisi setimbang (posisi setimbang ketika x = 0). Secara matematis ditulis :
F = -kx
Persamaan ini sering dikenal sebagai hukum hooke dan dicetuskan oleh paman Robert Hooke. k adalah konstanta dan x adalah simpangan. Hukum Hooke akurat jika pegas tidak ditekan sampai kumparan pegas bersentuhan atau diregangkan sampai batas elastisitas. Tanda negatif menunjukkan bahwa gaya pemulih alias F mempunyai arah berlawanan dengan simpangan x. Ketika kita menarik pegas ke kanan maka x bernilai positif, tetapi arah F ke kiri (berlawanan arah dengan simpangan x). Sebaliknya jika pegas ditekan, x berarah ke kiri (negatif), sedangkan gaya F bekerja ke kanan. Jadi gaya F selalu bekeja berlawanan arah dengan arah simpangan x. k adalah konstanta pegas. Konstanta pegas berkaitan dengan kaku atau lembut sebuah pegas. Semakin besar konstanta pegas (semakin kaku sebuah pegas), semakin besar gaya yang diperlukan untuk menekan atau meregangkan pegas. Sebaliknya semakin lembut sebuah pegas (semakin kecil konstanta pegas), semakin kecil gaya yang diperlukan untuk meregangkan pegas. Untuk meregangkan pegas sejauh x, kita akan memberikan gaya luar pada pegas, yang besarnya sama dengan F = +kx. Pegas dapat bergerak jika terlebih dahulu diberikan gaya luar. Amati bahwa besarnya gaya bergantung juga pada besar x (simpangan).
Sekarang mari kita tinjau lebih jauh apa yang terjadi jika pegas diregangkan sampai jarak x = A, kemudian dilepaskan (lihat gambar di bawah).
 Setelah pegas diregangkan, pegas menarik benda kembali ke posisi setimbang (x=0). Ketika melewati posisi setimbang, benda bergerak dengan laju yang tinggi karena telah diberi percepatan oleh gaya pemulih pegas. Ketika bergerak pada posisi setimbang, gaya pegas = 0, tetapi laju benda maksimum.
Setelah pegas diregangkan, pegas menarik benda kembali ke posisi setimbang (x=0). Ketika melewati posisi setimbang, benda bergerak dengan laju yang tinggi karena telah diberi percepatan oleh gaya pemulih pegas. Ketika bergerak pada posisi setimbang, gaya pegas = 0, tetapi laju benda maksimum. Karena laju benda maksimum maka benda terus bergerak ke kiri. Gaya pemulih pegas kembali memperlambat gerakan benda sehingga laju benda perlahan-lahan menurun dan benda berhenti sejenak ketika berada pada x = -A. Pada titik ini, laju benda = 0, tetapi gaya pegas bernilai maksimum, di mana arahnya menuju ke kanan (menuju posisi setimbang).
Karena laju benda maksimum maka benda terus bergerak ke kiri. Gaya pemulih pegas kembali memperlambat gerakan benda sehingga laju benda perlahan-lahan menurun dan benda berhenti sejenak ketika berada pada x = -A. Pada titik ini, laju benda = 0, tetapi gaya pegas bernilai maksimum, di mana arahnya menuju ke kanan (menuju posisi setimbang).
 Benda tersebut bergerak kembali ke kanan menuju titik setimbang karena ditarik oleh gaya pemulih pegas tadi. Gerakan benda ke kanan dan ke kiri berulang secara periodik dan simetris antara x = A dan x = -A.
Benda tersebut bergerak kembali ke kanan menuju titik setimbang karena ditarik oleh gaya pemulih pegas tadi. Gerakan benda ke kanan dan ke kiri berulang secara periodik dan simetris antara x = A dan x = -A.

Besaran fisika pada Gerak Harmonik Sederhana pada pegas pada dasarnya sama dengan ayunan sederhana, yakni terdapat periode, frekuensi dan amplitudo. Jarak x dari posisi setimbang disebut simpangan. Simpangan maksimum alias jarak terbesar dari titik setimbang disebut amplitudo (A). Satu getaran Gerak Harmonik Sederhana pada pegas adalah gerak bolak balik lengkap dari titik awal dan kembali ke titik yang sama. Misalnya jika benda diregangkan ke kanan, maka benda bergerak mulai dari titik x = 0, menuju titik x = A, kembali lagi ke titik x = 0, lalu bergerak menuju titik x = -A dan kembali ke titik x = 0 (bingung-kah ? ![]() ). Dipahami perlahan-lahan ya…
). Dipahami perlahan-lahan ya…
Bagaimana osilasi pada pegas yang digantungkan secara vertikal ?
Pada dasarnya osilasi alias getaran dari pegas yang digantungkan secara vertikal sama dengan getaran pegas yang diletakan horisontal. Bedanya, pegas yang digantungkan secara vertikal lebih panjang karena pengaruh gravitasi yang bekerja pada benda. Mari kita tinjau lebih jauh getaran pada pegas yang digantungkan secara vertikal…
 Pada pegas yang kita letakan horisontal (mendatar), posisi benda disesuaikan dengan panjang pegas alami. Pegas akan meregang atau mengerut jika diberikan gaya luar (ditarik atau ditekan). Nah, pada pegas yang digantungkan vertikal, gravitasi bekerja pada benda bermassa yang dikaitkan pada ujung pegas. Akibatnya, walaupun tidak ditarik ke bawah, pegas dengan sendirinya meregang sejauh x0. Pada keadaan ini benda yang digantungkan pada pegas berada pada posisi setimbang.
Pada pegas yang kita letakan horisontal (mendatar), posisi benda disesuaikan dengan panjang pegas alami. Pegas akan meregang atau mengerut jika diberikan gaya luar (ditarik atau ditekan). Nah, pada pegas yang digantungkan vertikal, gravitasi bekerja pada benda bermassa yang dikaitkan pada ujung pegas. Akibatnya, walaupun tidak ditarik ke bawah, pegas dengan sendirinya meregang sejauh x0. Pada keadaan ini benda yang digantungkan pada pegas berada pada posisi setimbang.
Berdasarkan hukum II Newton, benda berada dalam keadaan setimbang jika gaya total = 0. Gaya yang bekerja pada benda yang digantung adalah gaya pegas (F0 = -kx0) yang arahnya ke atas dan gaya berat (w = mg) yang arahnya ke bawah. Total kedua gaya ini sama dengan nol.
Gurumuda tetap menggunakan lambang x agar anda bisa membandingkan dengan pegas yang diletakan horisontal. Dirimu dapat menggantikan x dengan y. Resultan gaya yang bekerja pada titik kesetimbangan = 0. Hal ini berarti benda diam alias tidak bergerak.
Jika kita meregangkan pegas (menarik pegas ke bawah) sejauh x, maka pada keadaan ini bekerja gaya pegas yang nilainya lebih besar dari pada gaya berat, sehingga benda tidak lagi berada pada keadaan setimbang (perhatikan gambar c di bawah). Total kedua gaya ini tidak sama dengan nol karena terdapat pertambahan jarak sejauh x; sehingga gaya pegas bernilai lebih besar dari gaya berat. Karena terdapat gaya pegas (gaya pemulih) yang berarah ke atas maka benda akan bergerak ke atas menuju titik setimbang. (sambil lihat gambar di bawah ya).
Total kedua gaya ini tidak sama dengan nol karena terdapat pertambahan jarak sejauh x; sehingga gaya pegas bernilai lebih besar dari gaya berat. Karena terdapat gaya pegas (gaya pemulih) yang berarah ke atas maka benda akan bergerak ke atas menuju titik setimbang. (sambil lihat gambar di bawah ya). Pada titik setimbang, besar gaya total = 0, tetapi laju gerak benda bernilai maksimum (v maks), sehingga benda bergerak terus ke atas sejauh -x. Laju gerak benda perlahan-lahan menurun, sedangkan besar gaya pemulih meningkat dan mencapai nilai maksimum pada jarak -x. Setelah mencapai jarak -x, gaya pemulih pegas menggerakan benda kembali lagi ke posisi setimbang (lihat gambar di bawah). Demikian seterusnya. Benda akan bergerak ke bawah dan ke atas secara periodik. Dalam kenyataannya, pada suatu saat tertentu pegas tersebut berhenti bergerak karena adanya gaya gesekan udara.
Pada titik setimbang, besar gaya total = 0, tetapi laju gerak benda bernilai maksimum (v maks), sehingga benda bergerak terus ke atas sejauh -x. Laju gerak benda perlahan-lahan menurun, sedangkan besar gaya pemulih meningkat dan mencapai nilai maksimum pada jarak -x. Setelah mencapai jarak -x, gaya pemulih pegas menggerakan benda kembali lagi ke posisi setimbang (lihat gambar di bawah). Demikian seterusnya. Benda akan bergerak ke bawah dan ke atas secara periodik. Dalam kenyataannya, pada suatu saat tertentu pegas tersebut berhenti bergerak karena adanya gaya gesekan udara. Semua benda yang bergetar di mana gaya pemulih F berbanding lurus dengan negatif simpangan (F = -kx), maka benda tersebut dikatakan melakukan gerak harmonik sederhana (GHS) atau Osilasi Harmonik Sederhana (OHS).
Semua benda yang bergetar di mana gaya pemulih F berbanding lurus dengan negatif simpangan (F = -kx), maka benda tersebut dikatakan melakukan gerak harmonik sederhana (GHS) atau Osilasi Harmonik Sederhana (OHS).
Contoh soal 1 :
Sebuah benda digantungkan pada sebuah tali yang digantung vertikal. Benda tersebut ditarik ke samping dan dilepaskan sehingga benda bergerak bolak balik di antara dua titik terpisah sejauh 20 cm. Setelah 20 detik dilepaskan, benda melakukan getaran sebanyak 40 kali. Hitunglah frekuensi, periode dan amplitudo getaran benda tersebut.
Panduan jawaban :
a) Frekuensi adalah banyaknya getaran yang dilakukan benda selama satu detik. Benda melakukan getaran sebanyak 40 kali selama 20 detik. Dengan demikian, selama 1 detik benda tersebut melakukan getaran sebanyak 2 kali (40 / 20).
b) Periode adalah waktu yang dibutuhkan untuk melakukan satu getaran (T).
T = 1/f = ½ = 0,5 sekon
Jadi benda melakukan satu getaran selama 0,5 detik.
c) Amplitudo adalah simpangan maksimum diukur dari titik keseimbangan. Karena benda bergerak bolak balik alias melakukan getaran di antara dua titik terpisah sejauh 20 cm, maka amplitudo getaran benda adalah setengah dari lintasan yang dilalui benda tersebut. Dengan demikian, amplitudo = ½ (20 cm) = 10 cm
Contoh soal 2 :
Sebuah benda digantungkan pada sebuah pegas dan berada pada titik kesetimbangan. Benda tersebut ditarik ke bawah sejauh 5 cm dan dilepaskan. Jika benda melalui titik terendah sebanyak 10 kali selama 5 detik, tentukanlah frekuensi, periode dan amplitudo getaran benda tersebut.
Panduan jawaban :
a) Frekuensi
Frekuensi adalah banyaknya getaran yang dilakukan benda selama satu detik. Pada soal dikatakan bahwa benda tersebut melewati titik terendah sebanyak 10 kali selama 5 detik. Agar benda bisa melewati titik terendah maka benda tersebut pasti melakukan getaran (gerakan bolak balik dari titik terendah menuju titik tertinggi dan kembali lagi ke titik terendah). Karena benda melewati titik terendah sebanyak 10 kali selama 5 detik maka dapat dikatakan bahwa benda melakukan getaran sebanyak 10 kali selama 5 detik. Dengan demikian, selama 1 detik benda tersebut melakukan getaran sebanyak 2 kali (10 / 5).
b) Periode
Periode adalah waktu yang dibutuhkan untuk melakukan satu getaran (T).
T = 1/f = ½ = 0,5 sekon
Jadi benda melakukan satu getaran selama 0,5 detik.
c) Amplitudo adalah simpangan maksimum diukur dari titik keseimbangan. Pada soal di atas, amplitudo getaran benda adalah 5 cm
Contoh soal 3 :
Sebuah sedan bermassa 1200 kg ditumpangi 3 orang yang memiliki massa total 200 kg. Pegas mobil tersebut tertekan sejauh 5 cm. Anggap saja percepatan gravitasi = 10 m/s2
Hitunglah :
a) konstanta pegas mobil tersebut
b) berapa jauh pegas sedan tersebut tertekan jika sedan dinaiki 4 orang dan bagasinya dipenuhi dengan muatan sehingga total massa adalah 300 kg ?
Panduan jawaban :
Pegas sedan mulai tertekan ketika dimuati beban bermassa 200 kg. Dengan demikian massa sedan tidak disertakan dalam perhitungan, karena ketika sedan tidak dimuati beban, pegas sedan berada pada posisi setimbang.
a) konstanta pegas
k = F/x = (200 kg)(10 m/s2) / (5 x 10-2 m) = …. lanjUtkaN!
b) apabila sedan dimuati beban bermassa 300 kg, maka
x = F/k = (300 kg)(10 m/s2) / (4 x 104 N/m) = ….lanjUtk
Referensi :
Giancoli, Douglas C., 2001, Fisika Jilid I (terjemahan), Jakarta : Penerbit Erlangga
Halliday dan Resnick, 1991, Fisika Jilid I, Terjemahan, Jakarta : Penerbit Erlangga
Tipler, P.A.,1998, Fisika untuk Sains dan Teknik-Jilid I (terjemahan), Jakarta : Penebit Erlangga
Young, Hugh D. & Freedman, Roger A., 2002, Fisika Universitas (terjemahan), Jakarta : Penerbit Erlangga
Getaran

Getaran adalah suatu gerak bolak-balik di sekitar kesetimbangan. Kesetimbangan di sini maksudnya adalah keadaan dimana suatu benda berada pada posisi diam jika tidak ada gaya yang bekerja pada benda tersebut. Getaran mempunyai amplitudo (jarak simpangan terjauh dengan titik tengah) yang sama.
daftar isi |
.Jenis getaran
Getaran bebas terjadi bila sistem mekanis dimulai dengan gaya awal, lalu dibiarkan bergetar secara bebas. Contoh getaran seperti ini adalah memukul garpu tala dan membiarkannya bergetar, atau bandul yang ditarik dari keadaan setimbang lalu dilepaskan.
Getaran paksa terjadi bila gaya bolak-balik atau gerakan diterapkan pada sistem mekanis. Contohnya adalah getaran gedung pada saat gempa bumi.
.Analisis getaran
Dasar analisis getaran dapat dipahami dengan mempelajari model sederhana massa-pegas-peredam kejut. Struktur rumit seperti badan mobil dapat dimodelkan sebagai "jumlahan" model massa-pegas-peredam kejut tersebut. Model ini adalah contoh osilator harmonik sederhana.
.Getaran bebas tanpa peredam
Pada model yang paling sederhana redaman dianggap dapat diabaikan, dan tidak ada gaya luar yang mempengaruhi massa (getaran bebas).
Dalam keadaan ini gaya yang berlaku pada pegas Fs sebanding dengan panjang peregangan x, sesuai dengan hukum Hooke, atau bila dirumuskan secara matematis:
dengan k adalah tetapan pegas.
Sesuai Hukum kedua Newton gaya yang ditimbulkan sebanding dengan percepatan massa:
Karena F = Fs, kita mendapatkan persamaan diferensial biasa berikut:
Bila kita menganggap bahwa kita memulai getaran sistem dengan meregangkan pegas sejauh A kemudian melepaskannya, solusi persamaan di atas yang memerikan gerakan massa adalah:
Solusi ini menyatakan bahwa massa akan berosilasi dalam gerak harmonis sederhana yang memiliki amplitudo A dan frekuensi fn. Bilangan fn adalah salah satu besaran yang terpenting dalam analisis getaran, dan dinamakan frekuensi alami takredam. Untuk sistem massa-pegas sederhana, fn didefinisikan sebagai:
Catatan: frekuensi sudut ω (ω = 2πf) dengan satuan radian per detik kerap kali digunakan dalam persamaan karena menyederhanakan persamaan, namun besaran ini biasanya diubah ke dalam frekuensi "standar" (satuan Hz) ketika menyatakan frekuensi sistem.
Bila massa dan kekakuan (tetapan k) diketahui frekuensi getaran sistem akan dapat ditentukan menggunakan rumus di atas.
.Getaran bebas dengan redaman
Bila peredaman diperhitungkan, berarti gaya peredam juga berlaku pada massa selain gaya yang disebabkan oleh peregangan pegas. Bila bergerak dalam fluida benda akan mendapatkan peredaman karena kekentalan fluida. Gaya akibat kekentalan ini sebanding dengan kecepatan benda. Konstanta akibat kekentalan (viskositas) c ini dinamakan koefisien peredam, dengan satuan N s/m (SI)
Dengan menjumlahkan semua gaya yang berlaku pada benda kita mendapatkan persamaan
Solusi persamaan ini tergantung pada besarnya redaman. Bila redaman cukup kecil, sistem masih akan bergetar, namun pada akhirnya akan berhenti. Keadaan ini disebut kurang redam, dan merupakan kasus yang paling mendapatkan perhatian dalam analisis vibrasi. Bila peredaman diperbesar sehingga mencapai titik saat sistem tidak lagi berosilasi, kita mencapai titik redaman kritis. Bila peredaman ditambahkan melewati titik kritis ini sistem disebut dalam keadaan lewat redam.
Nilai koefisien redaman yang diperlukan untuk mencapai titik redaman kritis pada model massa-pegas-peredam adalah:
Untuk mengkarakterisasi jumlah peredaman dalam sistem digunakan nisbah yang dinamakan nisbah redaman. Nisbah ini adalah perbandingan antara peredaman sebenarnya terhadap jumlah peredaman yang diperlukan untuk mencapai titik redaman kritis. Rumus untuk nisbah redaman (ζ) adalah
Sebagai contoh struktur logam akan memiliki nisbah redaman lebih kecil dari 0,05, sedangkan suspensi otomotif akan berada pada selang 0,2-0,3.
Solusi sistem kurang redam pada model massa-pegas-peredam adalah
Nilai X, amplitudo awal, dan φ, ingsutan fase, ditentukan oleh panjang regangan pegas.
Dari solusi tersebut perlu diperhatikan dua hal: faktor eksponensial dan fungsi cosinus. Faktor eksponensial menentukan seberapa cepat sistem teredam: semakin besar nisbah redaman, semakin cepat sistem teredam ke titik nol. Fungsi kosinus melambangkan osilasi sistem, namun frekuensi osilasi berbeda daripada kasus tidak teredam.
Frekuensi dalam hal ini disebut "frekuensi alamiah teredam", fd, dan terhubung dengan frekuensi alamiah takredam lewat rumus berikut.
Frekuensi alamiah teredam lebih kecil daripada frekuensi alamiah takredam, namun untuk banyak kasus praktis nisbah redaman relatif kecil, dan karenanya perbedaan tersebut dapat diabaikan. Karena itu deskripsi teredam dan takredam kerap kali tidak disebutkan ketika menyatakan frekuensi alamiah.
RUMUS_RUMUS KALOR
Kalor adalah bentuk energi yang berpindah karena perubahan suhu (Δt).
Daftar |
. Kalor jenis
Rumus:

dengan ketentuan:
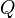 = Kalor yang diterima suatu zat (Joule, Kilojoule, Kalori, Kilokalori)
= Kalor yang diterima suatu zat (Joule, Kilojoule, Kalori, Kilokalori) = Massa zat (Gram, Kilogram)
= Massa zat (Gram, Kilogram) = Kalor jenis (Joule/kilogram°C, Joule/gram°C, Kalori/gram°C)
= Kalor jenis (Joule/kilogram°C, Joule/gram°C, Kalori/gram°C) = Perubahan suhu (°C) → (t2 - t1)
= Perubahan suhu (°C) → (t2 - t1)
Untuk mencari kalor jenis, rumusnya adalah:
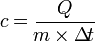
Untuk mencari massa zat, rumusnya adalah:

.Kapasitas kalor
Kapasitas kalor adalah banyaknya kalor yang dibutuhkan oleh benda untuk menaikkan suhunya 1°C.
Rumus kapasitas kalor:
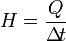
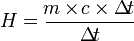

dengan syarat:
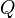 = Kalor yang diterima suatu zat (Joule, Kilojoule, Kalori, Kilokalori)
= Kalor yang diterima suatu zat (Joule, Kilojoule, Kalori, Kilokalori) = Kapasitas kalor (Joule/°C)
= Kapasitas kalor (Joule/°C) = Massa zat (Gram, Kilogram)
= Massa zat (Gram, Kilogram) = Kalor jenis (Joule/kilogram°C, Joule/gram°C, Kalori/gram°C)
= Kalor jenis (Joule/kilogram°C, Joule/gram°C, Kalori/gram°C) = Perubahan suhu (°C) → (t2 - t1)
= Perubahan suhu (°C) → (t2 - t1)
.Kalor lebur
Rumus:

dengan ketentuan:
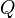 = Kalor yang diterima suatu zat (Joule, Kilojoule, Kalori, Kilokalori)
= Kalor yang diterima suatu zat (Joule, Kilojoule, Kalori, Kilokalori) = Massa zat (Gram, Kilogram)
= Massa zat (Gram, Kilogram) = Kalor lebur zat (Joule/kilogram, Kilojoule/kilogram, Joule/gram)
= Kalor lebur zat (Joule/kilogram, Kilojoule/kilogram, Joule/gram)
.Kalor uap
Rumus:
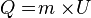
dengan ketentuan:
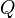 = Kalor yang diterima suatu zat (Joule, Kilojoule, Kalori, Kilokalori)
= Kalor yang diterima suatu zat (Joule, Kilojoule, Kalori, Kilokalori) = Massa zat (Gram, Kilogram)
= Massa zat (Gram, Kilogram) = Kalor uap zat (Joule/kilogram, Kilojoule/kilogram, Joule/gram)
= Kalor uap zat (Joule/kilogram, Kilojoule/kilogram, Joule/gram)
Contoh Soal :
Berapa energi kalor yang diperlukan untuk menguapkan 5 Kg air pada titik didihnya, jika kalor uap 2.260.000 Joule/Kilogram ?
Jawab :
Diketahui : m = 5 Kg
U = 2.260.000 J/Kg
Ditanyakan : Q =..... ?
Jawab Q = m x U
= 5 Kg x 2.260.000 J/Kg
= 11.300.000 J
= 11,3 x 106 J
.Asas Black
Rumus:
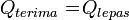 Asas Black : Jumlah kalor yang diterima sama dengan jumlah kalor yang dilepas
Asas Black : Jumlah kalor yang diterima sama dengan jumlah kalor yang dilepas